Exponents are a basic math tool that you learn in Pre-algebra, but many people struggle with them all the way through calculus! This is understandable given how difficult exponents are, let alone related operations like fractions and radicals can be. But that’s all the more reason to crush them. You really want to leave Pre-Algebra with a rock-solid understanding of exponents. In this article, we are going to discuss the properties of exponents as well as their purpose.
What are Exponent Rules?
The exponent rules describe how to solve various equations that, as you might expect, contain exponents. However, there are several types of exponent equations, which can be intimidating at first. However, as with most math strategies, there are teaching strategies that can be used to make exponent rules easier to understand.
Outcome of power rule
Keep the bases the same when multiplying two bases of the same value, and then add the exponents together to get the solution.
Power quotient rule
Multiplication and division are diametrically opposed; similarly, the quotient rule is the inverse of the product rule.
Keep the base constant when dividing two bases of the same value, and then subtract the exponent values.
The Power Rule
This rule explains how to solve equations in which one power is raised by another.
Product power rule
When multiplying any base by an exponent, distribute the exponent to each part of the base.
The efficacy of a quotient rule
A quotient is simply the result of dividing two quantities. You are increasing a quotient by a power in this rule. The exponent, like the power of a product rule, must be distributed to all values within the brackets to which it is attached.
The rule of zero power
Any number raised to the power of zero equals one.
The rule of negative exponents
When a number is raised by a negative exponent, convert it to a reciprocal to make the exponent positive. Don’t use the negative exponent rules to convert the base to a negative number.
What are Exponents?
There is no distinction between exponents and powers. So, exponents are also known as powers, and adding an exponent to something is the same as elevating it to the level of power. Exponents are simply a shortcut for indicating repeated multiplication of the same thing.
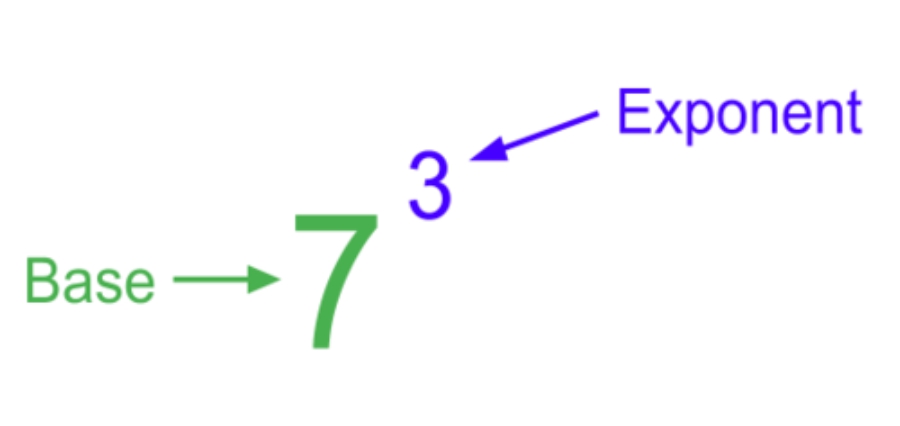
When you see an exponential function, you’ll notice the larger number at the bottom, followed by a small number in the upper right-hand corner. The large number at the bottom is known as the ‘base,’ and the small number in the corner is known as the exponent. You’re always adding the exponent to the base.
What is the Purpose of Exponents?
Exponents are useful in math because they allow us to shorten something that would otherwise be extremely long to write. If we wanted to express the product of x multiplied by itself 7 times in mathematics, we’d only be able to write it as xxxxxxx, x multiplied by itself 7 times in a row if we didn’t use exponents. So, we need a different way to express that value, which is where exponents come in. We can write x instead of x multiplied by itself 7 times. 7.
Scientific Notation
Scientific notation is the standard way of writing extremely large or extremely small numbers. Numbers are written using decimal and powers of ten in this. When a number from 0 to 9 is multiplied by a power of 10, it is said to be written in scientific notation. When a number is greater than one, the power of ten is a positive exponent; when a number is less than one, the power of ten is negative. For instance, 560000 = 5.6 105, and 0.00736567 = 7.36567 10-3.
To understand the topic in a fun and exciting manner, you can visit the Cuemath website.